Automated Lean Proofs for Every Type

Wouldn’t it be nice if every proof was automated by something that shortens the proof and works reliably 100% of the time? This summer, during my internship at Galois, I explored whether one of my favorite tools, SMT solvers, could provide that very solution

As part of a project aimed at verifying the frontend of the Jolt zkVM, we used an SMT solver to automate Lean proofs, saving over 6,800 lines of Lean code that would have been otherwise written by hand. Our results point towards the possibility and need of a more general framework for type translation in Lean. Read on to learn about the novel tactic we built, the (many) challenges we faced, and how one (maybe you?) can avoid them in the future! 

So, What is this All Purpose Solution? 

When doing research in Satisfiability Modulo Theories (SMT) solvers, it is easy to become a bit of an SMT solver fanatic, and find ways to use it for every tough decision …

- Deciding satisfiability of Bitvector conjunctions and disjunctions? SMT solvers!
- Deciding satisfiability of Integer equalities and inequalities? SMT solvers!
- Deciding what to have for lunch? SMT solvers! (maybe not) 

While SMT solvers clearly have their limits (e.g: they can’t help with lunch decisions or Higher Order Logic), they remain an incredibly powerful technology that can automate hours of painstaking manual labor. At a high level, an SMT solver acts like a crystal ball for logic: given a first order logical formula, it tells you whether that formula is always false or which variable assignment makes it true. In practice, SMT solvers let engineers offload a huge amount of symbolic reasoning.

Okay fine, SMT is not enough… 

However, when we want to prove theorems about real world software systems, we rarely reach for an SMT solver. Instead, we use an interactive theorem prover (ITP), like Lean. In an ITP the user drives the proof: deciding which lemma to apply, what variable to induct on and which definition to unfold. This makes ITPs far more expressive and useful than SMT solvers, but also more cumbersome for users. A query that an SMT solver could solve in seconds may take many lines of manually written Lean proof steps.

Ideally we want to be able to leverage both the automation and speed of SMT solvers and the expressivity and interactivity of Lean. 

The Bridge Between Lean and SMT 

While combining SMT solvers and Lean sounds like the perfect solution, in practice, it is not so simple. 

When an SMT solver says: “yes, this is always false,” Lean needs a way to make sure the solver isn’t lying. And if the solver says: “here’s a satisfying assignment,” Lean needs to know what to do with this information.

Many researchers are tackling these foundational technical challenges (lean-smt, auto-smt). My question is slightly different: once we have a working bridge, is this enough? Can we really use an SMT solver to its full capacity inside Lean?

Spoiler: not quite yet. Not all types used in Lean directly correspond to types used in SMT, but there is reason to be optimistic. 

The Gap in the Bridge 

Thus, we arrive at my second obsession, types!

Lean has a very rich ecosystem with built in support for many types like: Nat, Int, Fin, ZMod, UInt16, etc. SMT solvers work with slightly smaller and different but still overlapping types: integers, bitvectors, finite fields, and others. Each of these comes with its own specialized decision procedure which is an algorithm that automatically solves queries over the corresponding type.

Some translations between Lean and SMT are straightforward: Int maps to SMT integers, ZMod p maps to a finite field of order p. But others are ambiguous (Fins, UInt16 etc). Furthermore, a program might use one type to represent another.  For example, a Lean user might use integers for booleans : 0 for false, 1 for true. In this case, an SMT solver would be way more effective using a boolean decision procedure, instead of an integer one.

This mismatch means that if we want Lean & SMT automation to truly work, a technical bridge like auto-smt and lean-smt is not enough. We also need a way to give users the ability to choose their SMT theories and encodings. While an SMT solver should figure this out automatically, handing the control back to the user allows us to leverage the interactive part of an interactive theorem prover, without putting too much burden on the user. After all, users know their programs best, and they’re experts at inventing abstractions, optimizations, and custom types that not even other humans, let alone an automated solver, could reliably guess the meaning of every time.

Why is translation to SMT so hard?

Since the most effective decision procedures are highly specialized, translation often entails taking a ‘larger’ type and showing that it fits into a ‘smaller’ type. Think back to integers and booleans. If integers in our Lean proof represent booleans, we need to show that all integer variables are constrained by 0 and 1 and no operation makes us exit the space. This requires expert knowledge about the types involved and fairly complex range analysis. 

Finally my actual project! 

My project this summer was to help verify the frontend of the Jolt zkVM. Jolt is a zero-knowledge virtual machine that converts bitvector programs into finite field statements to allow users to quickly verify program execution. To do this efficiently, Jolt uses lookup tables where it equates bit vector operations (like AND, XOR, PEXT) to corresponding field operations. But here is the catch, the finite field elements are not really fields, instead they represent bits.

This means that using an SMT finite field decision procedure is not only superfluous but actually infeasible as the inequalities to constrain the elements to be between 0 or 1 would overwhelm the finite field solver. Instead, my team at Galois and I built a tactic that automatically translates ZMod to Nat to BitVectors and then calls an SMT based bit vector solver bv_decide.

The result? On 10 randomly sampled Jolt lookup tables we solved all the queries in under 3 minutes, while the finite field decision procedure timed out on all but one. This result becomes even more impressive if we consider the fact that the SMT solver is written in highly specialized C++ code, while our tactic is written in Lean which adds a lot more overhead. 

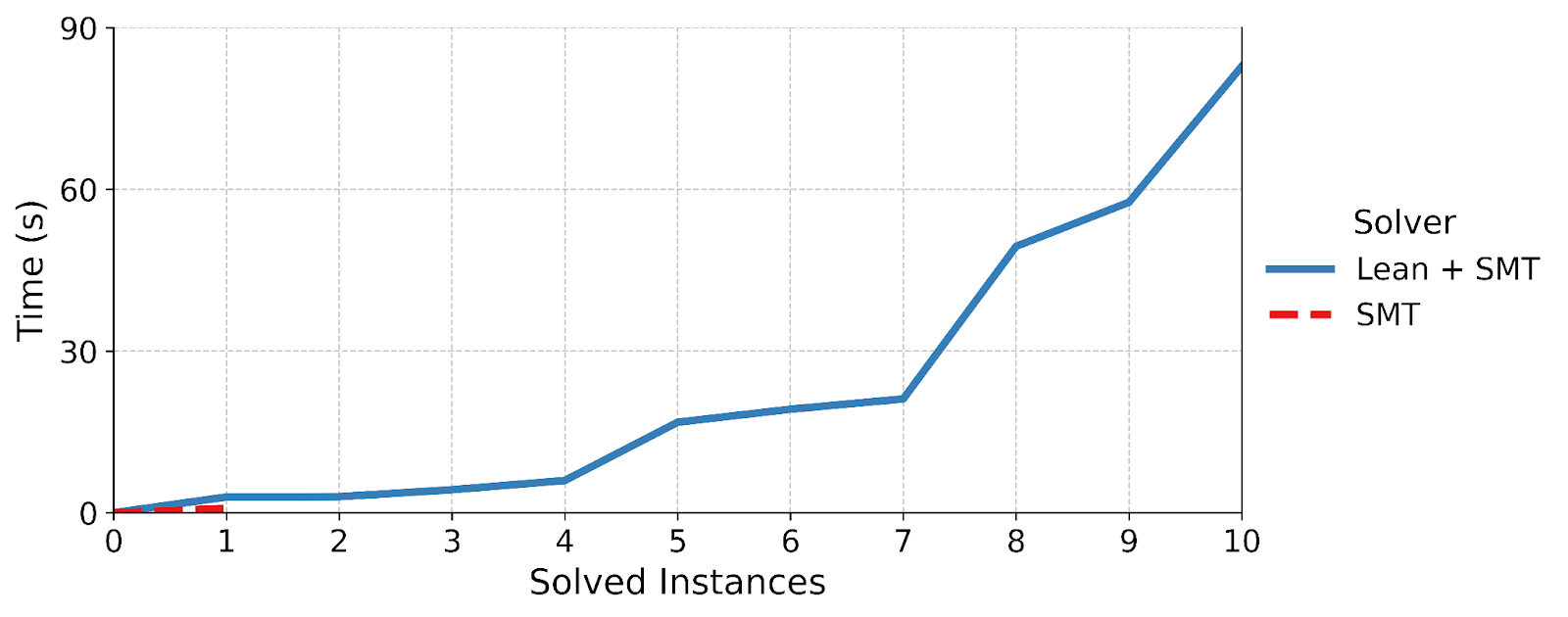
At the beginning of the internship I wrote the proof for translation of XOR (one of the simpler instructions) from finite field elements to bits manually. It took me about 213 lines of code and ten hours. Multiplying this by the 32 Jolt look up tables we had to verify,¹ our tactic saved me over 6,800 lines of code and 320 hours of work. Whef!!! 

While the solutions we developed for translating from larger to smaller types were type-specific, I believe our approach points toward the possibility of a more general framework for type translation. 

Project Hurdles

To translate from ZMod To BitVectors,  we overcame a two main challenges: 

1. Ensuring non-negativity of operations.
2. Ensuring boundedness of results, i.e. all outputs remain <2^W where W is some bitwidth.

For both of these problems Lean has well developed lemmas that reason about the ranges of variables, however they are not enough as they do not consider variable dependencies. For example lets say we want to show that given two natural numbers variables x, y, the following implication holds:  

(1 ≥ y, x, ≥ 0  ) → ( x+y - x*y) ≥ 0 

While this is true, no Lean lemma will allow you to prove it automatically,  without writing a proof by hand. Another way we could try to automate the proof is to use case analysis, and evaluate the equation at every variable value. The problem here is that some of the Jolt look up tables contain more than 64 variables resulting in 2^64 cases. If each case took 1 second, it would take about 584.9 billion years for our translation to finish, which is longer than my lifetime, much less my summer internship at Galois… 

Instead our solution was to use both. We traversed the AST of Jolt expressions using Lean lemmas and used case analysis once we arrived at an equation with two variables and subtraction, as it is here where variable dependencies play a large role. 

Could we translate every type to SMT?

To come up with our approach, we combined the way Lean would solve the problem with the way an SMT solver would. While each Lean type has its specific nuances, this hybrid method allowed us to fully leverage the type specifics needed for type translation. However there are cases where our method falls short and a general principled framework for type translation remains an open problem. 

While our tactic will save time in the future, it took a long time to build and develop. Yet its underlying pattern could apply to a lot of type translation instances. My hope is in the future a Lean type translation tactic would take a couple of hours instead of an entire summer to write. Such a framework would allow researchers to experiment more freely with using SMT in Lean and bring us closer to a world where automated Lean proofs for every type are an everyday reality.  

In our project we wrote code to traverse Lean AST supplying the range analysis lemmas needed for the specific types we used. We then relied on a bitvector specific decision procedure (bit blasting) to solve edge cases of variable dependencies. The first step could be generalized with the user supplying the type specific Lean lemmas. And the second, as SMT solver support improves could be handled by an SMT solver, or if an SMT solver is not enough, a user could specify the procedure necessary to handle variable dependencies (induction, split by cases etc etc).  More research is needed to see if this approach is feasible. 

Reflections 

It was very satisfying to see 32 bit Jolt zkVM proofs finish in a couple of minutes with just one line of code. It points towards a world, where a verification of real world systems could take days instead of years. While work on AI is also moving toward the same goal of automated proofs, it is complementary as opposed to competing. SMT tactics have the potential to aid both humans and AI: by making proofs smaller, faster and easier to maintain. However, as this summer showed there is a lot of work that we as a community (academia and industry) need to do to make this a reality.

Prior to this summer, I hadn’t written a single line of Lean code. I still wouldn’t call myself an expert, but along the way I uncovered a novel research direction that I never would have discovered without working on a real-world problem.  To me, this is the real merit of doing an internship at a place like Galois,at the intersection of industry and academia. Sometimes the road to a good project is paved with 6,800 lines of Lean code you’d rather not write and colleagues who challenge you to explore new research areas, solve hard problems, and discover creative solutions that only emerge at the intersection of domains. 

‍

Footnotes

1. From original Jolt paper and from Twist and Shout.

‍